
Zawartość
W przeciwieństwie do tego, co może sądzić wielu niezadowolonych uczniów, podstawowa geometria jest codziennie używana w ważnych i praktycznych dziedzinach. Podstawy geometrii są ważne, od dużych projektów inżynierii lądowej po proste obliczenia dekoracji. Jednym z najbardziej znanych i przydatnych zastosowań geometrii jest użycie twierdzenia Pitagorasa. Dowiedz się, jak go używać, aby znaleźć przeciwprostokątną w trójkącie prostokątnym.
Krok 1
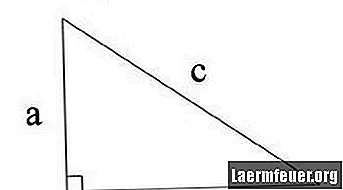
Uzyskaj wartości boków, które tworzą kąt prosty (90 stopni) trójkąta. Nazwiemy te wartości „a” i „b”. Zobacz ilustrację 1.
Krok 2
Zastąp wartości „a” i „b” w poniższym równaniu: a ^ 2 + b ^ 2 = c ^ 2 gdzie (^ 2) oznacza „do kwadratu”.
Krok 3
Oblicz wynik równania.
Krok 4
Weź wynik równania (c ^ 2) i oblicz jego pierwiastek kwadratowy.
Krok 5
Wynikiem równania jest „c”, które jest równe długości przeciwprostokątnej trójkąta prostokątnego.