
Zawartość
Sieć trakcyjna to kształt, jaki przybiera kabel, gdy jest podparty na końcach i podlega tylko działaniu swojego ciężaru. Jest szeroko stosowany w budownictwie, zwłaszcza w mostach wiszących, a odwrócona sieć trakcyjna była używana od czasów starożytnych do budowy łuków. Krzywa łańcuchowa to hiperboliczna funkcja cosinus, która ma kształt „U” podobny do paraboli. Kształt konkretnej sieci trakcyjnej można określić na podstawie jej współczynnika skali.
Obliczanie sieci trakcyjnej
Krok 1
Oblicz standardową funkcję łańcuchową y = a cosh (x / a), gdzie y to y płaszczyzny kartezjańskiej, x to x płaszczyzny kartezjańskiej, cosh to hiperboliczna funkcja cosinus, a „a” to współczynnik skali.
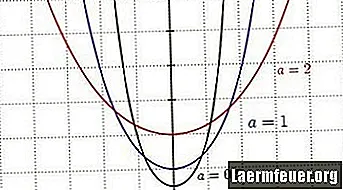
Krok 2
Obserwuj wpływ współczynnika skali na kształt sieci trakcyjnej. Można to traktować jako stosunek poziomego naprężenia w kablu do ciężaru kabla na jednostkę długości. Mniejszy współczynnik skali spowoduje wtedy głębszą krzywą.
Krok 3
Oblicz funkcję sieciową za pomocą alternatywnego równania. Równanie „y = a cosh (x / a)” można udowodnić jako matematyczny odpowiednik „y = a / 2 (e ^ (x / a) + e ^ (- x / a))”, w którym „e "jest podstawą logarytmu naturalnego i wynosi około 2,71828.
Krok 4
Oblicz funkcję dla sprężystej sieci trakcyjnej, takiej jak „y = yo / (1 + et)”, gdzie „yo” to masa początkowa na jednostkę długości, „e” to stała sprężystości, a „t” to czas. To równanie opisuje odbijającą się sprężynę zamiast wiszącego kabla.
Krok 5
Oblicz prawdziwy przykład sieci trakcyjnej. Funkcja „y = -127,7 cosh (x / 127,7) + 757,7” opisuje „Łuk św. Ludwika” (Łuk św. Ludwika), pomiary są podane w stopach.