
Zawartość
- Określ czas w powietrzu.
- Krok 1
- Krok 2
- Krok 3
- Krok 4
- Określ maksymalną wysokość
- Krok 1
- Krok 2
- Krok 3
- Określ przebytą odległość poziomą.
- Krok 1
- Krok 2
- Krok 3
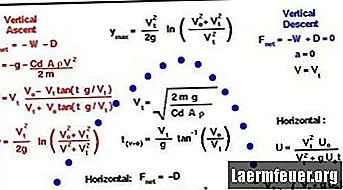
Oto metoda obliczania trajektorii pocisku, a konkretnie czasu w powietrzu, zasięgu i najwyższego punktu jego trajektorii. W tym przykładzie przyjęto pewne założenia w celu uproszczenia obliczeń: znikomy opór powietrza, brak wiatru i niewystarczająca odległość ostrzału, aby obrót Ziemi mógł zadziałać.
Określ czas w powietrzu.
Krok 1
Najpierw należy określić kształt łuku. Jeśli początkowo kąt jest w dół, wówczas wiadomo już, że najwyższym punktem jest pozycja strzelania. Nawet kąt skierowany do góry może mieć cel jako najwyższy punkt, niezależnie od tego, czy ten kąt jest płytki, czy ma wystarczającą wysokość (h). Można to określić w kroku czwartym, kiedy określa się czas antenowy.
Krok 2
Jeśli kąt „?” Szybkość wystrzeliwania jest taka, jaka mieści się między początkową trajektorią pocisku a poziomą, więc początkowa prędkość pionowa wynosi V (i) = V.sen?
Krok 3
Czas antenowy oblicza się za pomocą równania dla położenia h = V.sen? .T - (0,5) g.t ^ 2, gdzie g = 9,8 metra / sekundę ^ 2. Wszystkie zmienne są znane, z wyjątkiem czasu w powietrzu, t, więc można to rozwiązać za pomocą funkcji kwadratowej: ax ^ 2 + bx + c = 0, a zatem x = [-b ± √ (b ^ 2-4ac )] / 2a
Krok 4
Jeśli dozwolone jest więcej niż jedno rozwiązanie dla t, ponieważ h> 0, to pierwszy wynik odpowiada sytuacji, gdy wysokość = h na ścieżce wznoszenia, a drugi, gdy wysokość = h na ścieżce zejścia. Jeśli h <0, to jedyne rzeczywiste rozwiązanie dla t było dozwolone, a drugie jest ujemne.
Określ maksymalną wysokość
Krok 1
Jeśli? <0, to już wiadomo, że maksymalna wysokość to wysokość początkowa, h = 0.
Krok 2
Jeśli był więcej niż jeden moment t, w którym pocisk sięga h, to najmniejsze t odpowiada torze lotu, gdzie h jest najwyższym punktem. Największe t odpowiada punktowi osiągającemu wyższą wysokość przed powrotem do h, aby rozwiązać tę wysokość, użyj wzoru V (t) = V (0) - 9,8 t, aby znaleźć wartość t, gdy prędkość pionowa wynosi zero. Innymi słowy, przez jaki czas t, V.sen? = 9,8 t.?
Krok 3
Rozwiązując t i łącząc wzór na wysokość, mamy maksymalną wysokość: hm = V.sen? - 4,9 t ^ 2. To samo podejście jest stosowane dla rozwiązania maksymalnej wysokości, jeśli tylko jedno rozwiązanie dla t było dozwolone.
Określ przebytą odległość poziomą.
Krok 1
Aby określić odległość w poziomie pokonaną do czasu, gdy pocisk osiągnie wysokość h, najpierw oblicz początkową prędkość pocisku w poziomie: v (i) = V.cos (?).
Krok 2
Zastąp czas t, w którym pocisk osiągnie końcową wysokość, A, w pozycji wzoru używając prędkości poziomej: A = V. cosΘ.t. Zakładając, że po prawej stronie nie ma oporu powietrza ani członu przyspieszenia.
Krok 3
Jeśli wystąpił więcej niż jeden czas t, gdy wysokość była wyrażona w h, wówczas dwie pozycje „A” będą ważne, z najwyższym osiągniętym punktem hm dla mniejszego z dwóch „A”. Poziome i pionowe pozycje końcowe oraz najwyższy osiągnięty punkt są teraz znane, określając w ten sposób trajektorię pocisku.